7. Listor och pekare
Vi hade ett litet problem när vi skapade ‘textvariabler’. Vi var tvungna att skapa ett antal char-variabler i rad i minnet och använda ett gemensamt namn för dessa. Detta löste vi genom att använda en lista.
|
Definition: En lista är ett antal variabler
av samma datatyp, vilka ligger i rad i minnet, samt har ett gemensamt
namn. Man anger vilken variabel man avser genom att ange namnet och ett
index inom hakparenteser.
|
Man deklarerar en lista med hjälp av följande syntax:
datatyp listnamn[antal element];
Varför skulle man då behöva en lista (bortsett från problemet med texter, vilket vi sett tidigare)? Vi kan ju ta och titta på hur man skulle kunna skriva en del av ett program, i vilken man hanterar datum. Man behöver ofta veta hur många dagar det är i en månad. Vi skulle ju kunna deklarera 12 variabler med namnen iManad1, iManad2, etc. Sedan kan vi skriva till exempel en switch på en variabel som innehåller månadens nummer. Detta blir klumpigt:
int iManad1 = 31, iManad2 = 28, iManad3 = 31, iManad4 = 30;
int iManad5 = 31, iManad6 = 30, iManad7 = 31, iManad8 = 31;
int iManad9 = 30, iManad10 = 31, iManad11 = 30, iManad12 = 31;
int iIndex, iAntDagar;
...
switch (iIndex)
{
case 1:
iAntDagar = iManad1;
break;
case 2:
iAntDagar = iManad2;
break;
case 3:
iAntDagar = iManad3;
break;
case 4:
iAntDagar = iManad4;
break;
case 5:
iAntDagar = iManad5;
break;
case 6:
iAntDagar = iManad6;
break;
case 7:
iAntDagar = iManad7;
break;
case 8:
iAntDagar = iManad8;
break;
case 9:
iAntDagar = iManad9;
break;
case 10:
iAntDagar = iManad10;
break;
case 11:
iAntDagar = iManad11;
break;
case 12:
iAntDagar = iManad12;
break;
}
Allt detta bara för att vi vill skapa en tabell med antalet dagar per månad, plus att hämta antal dagar för en månad när vi vet vilket nummer månaden har.
Detta går att göra bekvämare med hjälp av en lista. En variabel är ett logiskt namn på en plats i minnet, vilket reserverats för variabelns typ. En lista är detsamma, men den reserverar utrymme för flera likadana variabler i rad, under ett och samma namn. Därigenom kan man använda samma namn, och indexera sig fram till rätt variabel. Exemplet ovan kan bli mycket lättare:
int iManad[12] = {31, 28, 31, 30, 31, 30,
31, 31, 30, 31, 30, 31};
int iIndex, iAntDagar;
...
iAntDagar = iManad[iIndex];
Här ser vi även hur man kan initiera en hel lista i samband med deklaration. Tidigare har vi lärt oss att initiera en variabel vid deklaration. Skillnaden ligger i att vi nu egentligen har flera variabler, och kan ange flera värden. Som synes i exemplet ovan anger man värden mellan klamrar "{}" och separerar dem med kommatecken. Vi ska strax titta mer på detta.
En liten egenhet med listor är att de börjar med index = 0, inte 1. Skulle vi lägga äkta månadsnummer i iIndex skulle sista raden behöva ändras till:
iAntDagar = iManad[iIndex - 1];
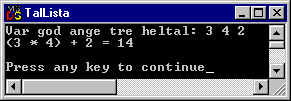
Låt oss testa en enkel lista. I ett tidigare kapitel multiplicerade vi två tal. Först deklarerades två heltalsvariabler, sedan ombads användaren mata in talen, och till sist multiplicerades talen, och resultatet skrevs ut på skärmen. Låt oss lösa uppgiften med en lista i stället. Listan ska innehålla tre element, ett för den ena faktorn, ett för den andra och ett för svaret. Så här skulle det kunna se ut:
#include <iostream.h>
void main()
{
int iTal[3];
cout << "Var god ange två heltal: ";
cin >> iTal[0] >> iTal[1];
iTal[2] = iTal[0] * iTal[1];
cout << iTal[0] << " * " << iTal[1] << " = " << iTal[2];
cout << "\n\n";
}
Som redan nämnts börjar listan med index 0, inte 1. Det betyder att vi i ovanstående exempel har tre element: 0, 1 respektive 2. Element nummer tre existerar inte, och om man använder det får man ´konstiga´ fel när man kör programmet. Det är programmerarens ansvar att inte använda ett index som är för stort eller för litet, det vill säga negativt.
|
Definition: En lista börjar alltid med
element nummer noll. Det tal man använder när man deklarerar listan är
alltså ett steg över listans övre gräns.
Deklarationen datatyp listnamn[n]; ger en lista med n stycken element, numrerade från noll till n minus 1, där n är ett valfritt heltal större än 1. |
Övningsuppgift 7.1.1:

Man deklarerar och initierar en lista enligt följande syntax:
datatyp listnamn[antal element] = {värde, ...};
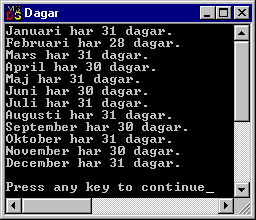
Ett exempel: en lista för antal dagar per månad:
short int manad[12] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
Man får inte ange fler värden än vad som ryms i listan. Kompilatorn ger i så fall ett felmeddelande "Too many initializers". Anger man för få värden kommer de överblivna elementen i slutet av listan att lämnas oinitierade.
Kompilatorns förmåga att räkna antalet initierare (de värden man anger) kan utnyttjas: Om man initierar en tabell med ett antal värden behöver man inte ange tabellens storlek, kompilatorn räknar antalet angivna värden själv:
short int manad[] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
Detta har vi faktiskt utnyttjat redan när vi skapade texter:
char cSkola[] = "Datortek";
I detta fall räknar kompilatorn till 8 tecken, lägger till ett sluttecken (en nolla), och tolkar det hela som om vi skrivit:
char cSkola[9] = "Datortek";
Det är t.o.m. så fint att kompilatorn ser att man anger datatypen char och initierar den med en textsträng. Den läser textsträngen och tolkar den som en kommaseparerad lista av enstaka tecken, vilket ju passar i en lista av typen char. Annars skulle man egentligen behövt skriva:
char cSkola[] = {´D´, ´a´, ´t´, ´o´, ´r´, ´t´, ´e´, ´k´, ´\0’};
Följande övningsuppgift demonstrerar hur cout använder sluttecknet (´\0´) till att avbryta utskriften på rätt ställe. Lägg märke till att utskriften inte avbryts i tid när den första utskriften utförs. Däremot blir det rätt efter rättning.
Övningsuppgift 7.2.1:
#include <iostream.h>
void main()
{
char cText[] = {'F', 'e', 'l', '!'};
cout << cText;
}
Övningsuppgift 7.2.2:
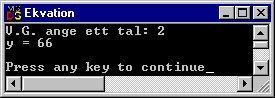
Hur skulle det då se ut om man ville göra en lista som beskriver ett schackbräde? Tänk dig att vi har ett bräde med alla pjäser i startposition. Vi har kanske bestämt att alla olika typer av pjäser representeras av ett nummer, t.ex vit dam = 1, vit kung = 2 etc. Eftersom det finns sex olika typer av pjäser, i två olika färger, behöver vi 12 olika värden, alltså kan man ha en lista av typen short.
Rutorna numreras traditionellt med siffror i "höjdled" och bokstäver i "sidled".
Nu bör vi inte indexera med bokstäver (även om det skulle gå att använda ascii-teknet minus 65), utan vi vill räkna med rad nummer 0 - 7 och kolumn 0 - 7.
Listan blir då en yta, den har två dimensioner. Det går alldeles utmärkt i C. Vi kan deklarera en lista med brädets rutor enligt följande exempel:
char ruta[8][8];
Det är alltså bara att lägga till flera dimensioner genom att räkna upp dem i rad (utan kommatecken). Syntaxen för en lista av valfritt antal dimensioner blir:
<datatyp> <listnamn>[<antal>]
[[<antal>]...];Övningsuppgift 7.3.1:
Som vi tidigare konstaterat finns det ingen datatyp för textsträngar i C. I de exempel vi tidigare har haft har vi i stället använt oss av en lista av datatypen char, och avslutat textsträngen med en byte som innehåller värdet NULL (‘\0’).
Hur blir det då om man vill skapa en lista med texter (t.ex. veckodagarnas namn)? Svaret blir naturligtvis en lista med två dimensioner, en dimension för veckodagar och en dimension för bokstäverna i varje dags namn:
char cDag[][8] = {"Måndag", "Tisdag", "Onsdag", Torsdag", "Fredag", "Lördag", "Söndag"};
Här klarar inte kompilatorn riktigt att räkna variabler i flera dimensioner, utan vi blir tvungna att i alla fall ange hur många bokstäver (+1) vi använder i den längsta arean (alla blir lika långa, men inte helt utfyllda). Den första dimensionen (antalet veckodagar) räknar den i alla fall åt oss om vi inte skriver något i den. Det vi anger blir alltså den andra dimensionen, som alltså representerar antalet tecken i varje text, plus avslutande nolla.
Övningsuppgift 7.3.2:
I kapitel 4 sades det att en variabel är en namngiven plats i minnet, avsedd att innehålla en viss typ av data. Anledningen till att man vill ha en namngiven plats är naturligtvis för att det är lättare att skriva programmen om man inte själv behöver hålla reda på var i datorns minne allt lagras. Dessutom kan program finnas på olika platser i minnet, så en variabel har inte alltid samma adress.
Det finns dock många situationer där man behöver använda adresser i stället för logiska namn. För detta finns det en speciell sorts variabel, pekaren. Pekaren är avsedd att innehålla en adress.
|
Definition: En pekare är en variabel avsedd
att innehålla en minnesadress. Pekaren är till för att peka på (bland
annat) data i minnet.
|
Man anger att en variabel används som en pekare genom att skriva en stjärna framför variabelnamnet. Så här ser till exempel en deklaration av en pekare ut:
char *pcText;
Här ovan deklarerades en pekare, och den är avsedd att peka på en variabel av typen char. Det finns flera orsaker till att pekaren måste 'märkas' med den typ den är avsedd att peka på, och vi kommer att stöta på en del av dessa under kursens gång. Prefixet pc avser pekare mot char. Det är högst rekommendabelt att använda tydliga prefix och variabelnamn.
Stjärnans placering är inte kritisk. Ovanstående deklaration kan skrivas på tre olika sätt med avseende på stjärnans placering. Stjärnan måste alltså bara stå mellan nyckelordet för datatypen och variabelnamnet:
char *pcText;
char* pcText;
char * pcText;
Härigenom kan man tala om pekaren *pcText, eller datatypen pekare mot char char*. I vissa situationer är ett skrivsätt att föredraga, i vissa ett annat. Det kan även vara en personlig smak vilket skrivsätt som man tycker är tydligast.
Om man vill tilldela minnet ett värde på den position pekaren pekar på skriver man en vanlig tilldelning, och använder stjärnan:
*pcText = 'A';
Förutsatt att pekaren pcText innehåller en lämplig adress kommer ovanstående tilldelningssats att lagra tecknet 'A' på den adressen. Faktum är att tilldelningen sker även om adressen är helt fel. Vissa operativsystem kan reagera och stänga programmet innan tilldelningen skett, om pekaren pekar på en adress som tillhör ett annat programs privata minnesutrymme. Pekare som pekar på fel plats är den i särklass vanligaste orsaken till programfel!
Hur tilldelar man då pekaren en adress? Genom en vanlig tilldelning, men utan att använda stjärnan. Det sker alltså på exakt samma sätt som när man tilldelar en 'vanlig' variabel ett värde:
pcText = 0x000afe42; // Adresser skrivs vanligen hexadecimalt.
Det är dock ovanligt att man tilldelar pekaren en absolut adress som i ovanstående exempel. Det vanligaste är att man använder pekare i samband med funktioner, men det kommer vi att titta på i nästa kapitel. Nu kan vi i stället försöka att tilldela pekaren adressen till en variabel vi redan deklarerat i vårt program. Hur var det nu vi fick adresssen till en variabel? Det har vi faktiskt redan nämnt som hastigast i kapitel 5; med hjälp av adressoperatorn, '&':
pcText = &cTecken;
Ovanstående förutsätter att även cTecken är deklarerad som char. Nu kan vi nå cTecken på två sätt. Nedanstående tilldelningar är ekvivalenta:
*pcText = 'B';
cTecken = 'B';
Övningsuppgift 7.4.1:
Hittills har vi använt ett index för att välja ett element i en lista. Som vi tidigare sett kan man använda s.k. ‘pekare’ för att tala om för programmet var i minnet det ska läsa eller skriva, i stället för att använda variabelnamnet. Pekaren kan också vara bra när man har en lista. Då kan man ha en pekare som pekar på de olika elementen i stället för att använda index.
Om nu t.ex ‘text[3]’ använder ett index = 3 till att peka på det fjärde elementet i variabeln text, vad är det då för skillnad på att använda index från att använda en pekare? Tekniskt sett är det visserligen en skillnad, men resultatet visar ingen skillnad alls, dock är det naturligtvis en skillnad: du skriver på ett annat sätt. Dock kommer kompilatorn och länkaren i slutändan att översätta det till en adress, och det är just vad en pekare innehåller. (Den tekniska skillnaden blir den att 'text[3]' översätts till en adress med en offset, ett avstånd framåt i minnet, det vill säga adressen till text[0] + 3 steg framåt, medan en direkt pekare innehåller den adress som blir resultatet efter ovanstående 'framåtstegning'.)
Det första elementet i en lista är t.ex. iDagar[0], d.v.s. alltid en nolla inom hakparanteserna. Adressen till en variabel får man m.h.a. adressoperatorn, ‘&’. T.ex. &iDagar[0]. Nu har man hittat på att förkorta detta i C. Man kan i stället skriva bara t.ex iDagar. Detta tolkas som &iDagar[0].
Detta är precis vad vi gjort när vi bett cout att skriva ut textsträngar. Se tidigare exempel. Nu ser vi att cout har två sätt att uppfatta char. Antingen som enstaka tecken eller som text. Vi kan ju prova skillnaden. Betrakta nedanstående program:
#include <iostream.h>
void main()
{
// Deklarera en 'textvariabel' och en teckenpekare:
char cTecken[] = "Putte Fnask";
char *cpTeckenPekare;
// Låt teckenpekaren peka på teckenvariabeln:
cpTeckenPekare = &cTecken[0];
// Skriv ut med stjärna (det borde ge samma effekt som att
// skriva ut cTecken):
cout << "cTecken innehåller: " << *cpTeckenPekare << "\n\n";
// Skriv ut utan stjärna (det borde tolkas som om det
// skulle finnas en nollterminerad textsträng där pekaren
// pekar, vilket det gör i detta fall):
cout << "cTecken innehåller: " << cpTeckenPekare << "\n\n";
}
Så här blir utskriften. Lägg märke till att cout 'känner av' om vi angivit en pekare till ett tecken (en char*) eller en text:
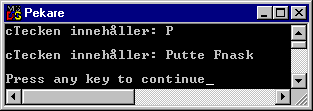
Vill man alltså att cout ska uppfatta en pekare som en pekare mot text ska man alltså inte använda stjärnan.
Att komma ihåg:
Vill man att en pekare, som pekar på ett element i en lista, ska peka på nästa element i listan, så ökar man pekarens värde med ett:
int * iPek;
int iTalLista[] = {1,5,2,65,12,8,0,-3};
iPek = iTalLista; // iPek pekar på första talet i listan (1).
iPek++; // iPek pekar på nästa tal i listan (5).
Men, säger du nu (om du hänger med ordentligt), ett heltal tar fyra bytes i minnet. Måste jag då inte öka pekarens värde, det vill säga adressen, med fyra i stället för ett? Det är där som vi har första nyttan av att pekaren har fått en datatyp. Kompilatorn ser att vi vill stega fram en pekare som är av datatypen 'int', och översätter i själva verket detta till programkod som ökar adressen i pekaren med fyra. Skulle vi skriva:
iPek += 2;
Så skulle kompilatorn översätta det till kod som ökar adressen i pekaren med åtta steg och så vidare.
Övningsuppgift 7.5.1:
Man kan kopiera ett tecken som en pekare 'pFran' pekar på till en position som en pekare 'pTill' pekar på:
*pTill = *pFran;
Om dessa pekar på två charlistor, kommer ett tecken att kopieras från den ena till den andra:
char Original[25] = "Denna text ska kopieras.";
char Kopia[25];
char *pFran = Original;
char *pTill = Kopia;
*pTill = *pFran;
Vill vi, så kan vi låta bägge pekarna peka på nästa tecken. Detta kan ske i samma programsats:
*pTill++ = *pFran++;
Observera att ökningen sker efter kopieringen. Vill vi att detta ska upprepas tills det avslutande nolltecknet i originaltexten har kopierats kan vi låta en while-slinga sköta detta. Den kan avbrytas när det kopierade värdet är noll:
while((*pTill++ = *pFran++) != 0);
Faktum är att vi inte ens behöver jämföra med talet noll. Noll är ju i sig själv det enda som är falskt, så egentligen räcker det med nedanstående variant:
while(*pTill++ = *pFran++);
Övningsuppgift 7.5.2:
Övningsuppgift 7.5.3:
En vanlig uppgift för en dator är att söka information. Vi ska ta och titta på hur man kan söka ett värde i en lista. Listan kan i så fall vara sorterad eller osorterad, varvid vi ställs inför två helt olika problem. Söker man en bok på biblioteket så står de sorterade efter ämneskoder, och därunder i bokstavsordning med avseende på författarens efternamn. Söker man en bok i min bokhylla får man stå ut med att de står helt i oordning.
Har man en osorterad lista finns det bara en sak att göra, och det är att titta på vart och ett av elementen tills man finner vad man söker. Detta kallas sekventiell sökning. Letar vi till exempel efter en bok i min bokhylla börjar man med att titta på den första boken, läsa titeln och jämföra med efterfrågad titel. Är de samma tar man boken och är nöjd, annars tittar man på nästa bok och så vidare, tills man hittat boken eller tills man kontrollerat alla böcker vilket nu kan tänkas inträffa först.
Har man en lista som är sorterad söker man informationen systematiskt. Ta till exempel telefonkatalogen. Vill man söka upp Clark Kent börjar man med att slå upp ungefär i mitten, eftersom 'K' är nästan i mitten av alfabetet. Antagligen finner man väl namn som börjar på 'N' eller 'O' eller någonstans däromkring. Sedan inser man att 'K' finns tidigare än där vi är, och att 'K' finns närmre nuvarande uppslag än början, varvid vi bläddrar tillbaka kanske en fjärdedel av den vänstra delen av katalogen. Sedan läser vi igen och tar ett nytt beslut att vända ett mindre antal sidor. Till sist har vi rätt sida, och med ett par snabba ögonkast upprepar vi metoden och finner 'Kent, Clark'. Om det finns fler än en Clark Kent letar vi sekventiellt tills vi känner igen till exempel adressen.
Denna form av sökning kallas binär eller hierarkisk.
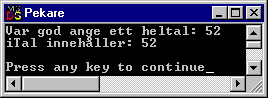
Låt oss börja med linjär sökning. Vi kan tänka oss att vi har en lista med olika talvärden i oordning. Listan kan exempelvis deklareras som
int iTal[16]:
![]()
Man kan till exempel söka talet -19. Då kan man börja med det första talet, 5 och jämföra det med -19. Eftersom det inte är detsamma tar vi nästa tal, -9 och jämför. Detta ska alltså pågå tills vi kommer till det element som innehåller värdet -19, varvid sökningen är klar.
Detta kan naturligtvis representeras av ett JSP-schema. Börja med ett block, vilket ska motsvara hela programmet:

Därefter delar vi upp problemet. Vi behöver en pekare eller ett index för att adressera listans olika element, och den ska initieras till 0 för att peka på det första elementet. Därefter kan vi iterera oss genom listan:
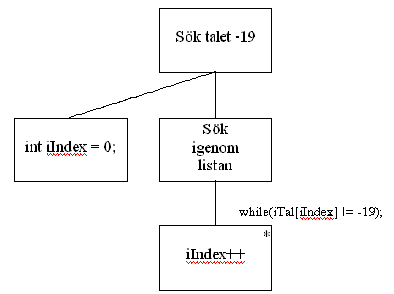
Observera att vi här inte hanterar fall där värdet saknas i listan. Detta exempel kan lätt skrivas i C++. Deklaration och initiering av själva listan finns också med här:
#include <iostream.h>
void main()
{
int iTal[16] = {5, -9, 28, 1, 255, -89, -19, 965,
758, 96, 102, 336, 9, 187, 62, 11};
int iIndex = 0;
while(iTal[iIndex] != -19) iIndex++; // Så här får man också skriva.
}
Det blev ju inte så komplicerat. Man kanske även skulle hantera situationer där det sökta talet inte finns i listan, och kanske göra något av att vi hittat talet. Så här kan man utöka exemplet:
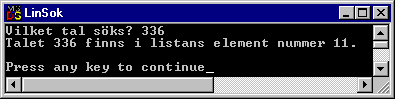
#include <iostream.h>
void main()
{
int iTal[16] = {5, -9, 28, 1, 255, -89, -19, 965, 758, 96, 102, 336, 9, 187, 62, 11};
int iIndex = 0;
int iSokTal;
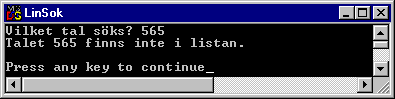
cout << "Vilket tal söks? ";
cin >> iSokTal;
while(iTal[iIndex] != iSokTal && iIndex < 16) iIndex++;
if(iIndex < 16)
{
cout << "Talet " << iSokTal
<< " finns i listans element nummer "
<< iIndex << ".";}
cout << "\n\n";
}
Testar vi detta kan det se ut till exempel så här:
Övningsuppgift 7.6.1:
Som vi tidigare sätt är det inte lättare att söka i en sorterad lista. Det blir tvärt emot svårare, eftersom vi måste utnyttja det faktum att listan är sorterad, för att göra en snabbare sökning. OK, det tar inte lång tid att söka bland 16 element i en lista, men om vi betänker att ett program normalt kanske söker bland miljontals element kan vi kanske förstå att det kan vara bra att försöka ta den genaste vägen. Låt oss därför sortera vår lista. (Vi kommer att titta mer på sorteringar i nästa avsnitt.)
![]()
Om man nu söker ett tal, skulle den linjära sökningen i medeltal kräva 8 läsningar i vår lista. Vi ska försöka minimera det antalet. Man kan till exempel börja med att läsa det mittersta talet. I vårt fall är det 28 (det kan bli 62 beroende på om vårt sätt att beräkna det mittersta elementet resulterar i element nummer 7 eller 8, vi har ju ett jämnt antal element). Genom att jämföra detta tal med det sökta talet kan man redan utesluta halva listan!
Låt oss åter söka talet -19. Det är mindre än 28, och därför vet vi att talet inte finns i något av elementen 7 till 15. Nu kan vi fortsätta att söka mittpunkten mellan element noll och element 6. Det blir element 3, vilken innehåller talet 1. Det blev andra läsningen.
Nu blir sökningen mellan element 0 och 2, och då får vi faktiskt träff redan på tredje läsningen. Hade det varit element 1 eller två hade sökningen krävt 4 läsningar. Det är i alla fall bättre med ett genomsnitt av 3 eller 4 läsningar i stället för 8, som linjär sökning gav. Faktum är att vinsten blir större ju fler element listan har.
Vi kan titta på ett JSP-schema för denna sökning. Börja med att initiera gränser, sätt indexet till en plats i listan för att inte få konstiga resultat:
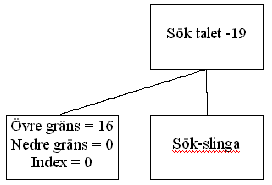
Här har jag använt tydliga namn, men eftersom de innehåller svenska tecken kan vi inte använda dem till programkoden. Hur ska vi sedan implementera, det vill säga genomföra, själva sökslingan? Så här kan man tänkta sig det:
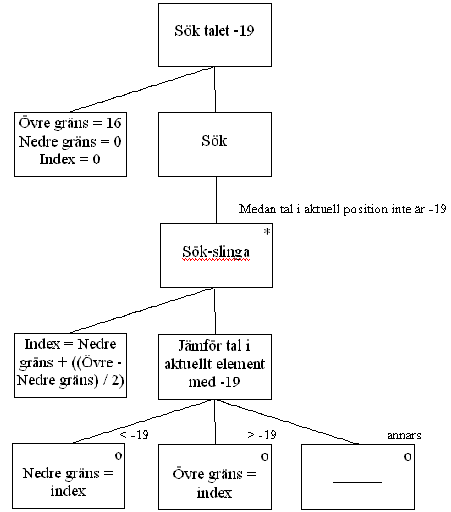
Övningsuppgift 7.6.2:
Övningsuppgift 7.6.3:
Vi ska nu titta på två olika sätt att sortera data. I föregående avsnitt hade vi en lista först i osorterad form:
![]()
... och sedan i sorterad form:
![]()
Lägg märke till att det är samma siffror i listan, de är bara sorterade i storleksordning. I förra avsnittet lovade jag visa hur man kan skriva ett program som sorterar en lista, och det ska vi som sagt se två varianter av nu. De två varianterna kallas urvalssortering respektive bubbelsortering. Urvalssorteringen ska vi titta på i detalj, men bubbelsorteringen kommer du delvis att lösa på egen hand.
Man börjar med att ta första talet och jämför det med alla efterföljande tal. Om man finner ett tal som är mindre än det första talet, så låter man dem byta plats. Vi behöver två index eller två pekare för att kunna manipulera listans element på detta sätt, här kallar jag dem i1 respektive i2:
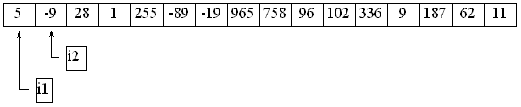
Nu byter alltså 5:an och -9:an plats, eftersom -9 är mindre än 5. Därefter händer ingenting förrän vi stöter på -89, som är mindre än -9. Observera att 1:an visserligen är mindre än 5:an, men femman är redan flyttad från första position, och ingår inte längre i jämförelsen:

Med denna metod kommer listan att se ut så här när i2 kommit till det sista elementet i listan:
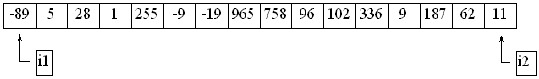
Resultatet blev alltså att det minsta talet hamnade längst till vänster. Kan vi använda samma metod till att få det näst minsta talet i det andra elementet? Klart! Det är bara att göra samma sak en gång till, men uteslut det första elementet denna gång. Börja så här:
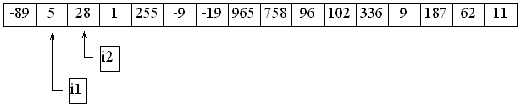
Upprepar man nu proceduren med i2, så kommer listan att bli så här:
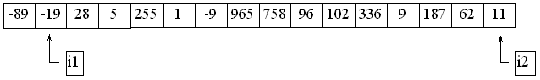
Nästa 'varv' resulterar sedan i detta utseende:
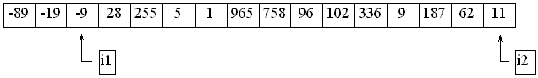
Fyll själv i hur det kommer att se ut efter nästa varv:

Och efter ytterligare ett:

Och en gång till:

Till sist kommer listan att se ut så här:

Detta ska vi nu lösa med hjälp av JSP. Först behöver vi en programslinga som itererar genom listan med i1. Därefter ska vi ha en programslinga som itererar igenom resten av listan för varje värde på i1. Till detta använder vi i2. Lämplig instruktion för programslinga är 'for', så detta introducerar jag redan i JSP-schemat. Först programslingan med i1. Observera att den ska sluta med näst sista elementet i listan. Det är ingen mening med att jämföra sista elementet med sig självt för att byta det om det är mindre än sig själv:

Sedan kan vi fortsätta med att förklara hur vi flyttar det lägsta av de efterföljande talen till den position som i1 pekar ut. Här passar det också bra med en for-slinga. Initieringen av i2 ska dock varje gång vara positionen efter den där i1 står, och vi initierar ju om denna slinga för varje varv i den föregående slingan.
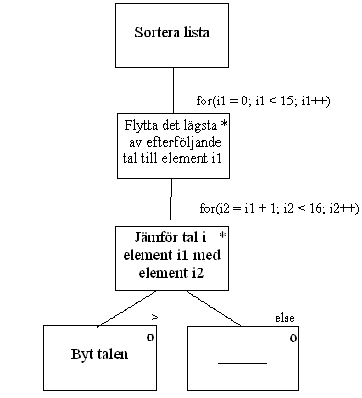
Detta kan lätt översättas till C++ kod. Om man lägger till utskrift av listan före och efter sortering blir källkoden så här:
#include <iostream.h>
void main()
{
int iTal[16] = {5, -9, 28, 1, 255, -89, -19, 965, 758, 96, 102, 336, 9, 187, 62, 11};
int i1, i2, temp;
// Visa listans utseende före sortering:
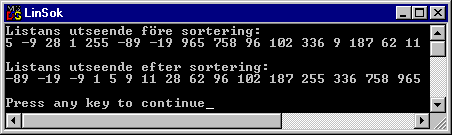
cout << "Listans utseende före sortering:\n";
for(i1 = 0; i1 < 16; i1++) cout << iTal[i1] << " ";
cout << "\n\n";
// Sortera listan:
for(i1 = 0; i1 < 15; i1++)
{
for(i2 = i1 + 1; i2 < 16; i2++)
{
if(iTal[i1] > iTal[i2])
{
temp = iTal[i1];
iTal[i1] = iTal[i2];
iTal[i2] = temp;
}
}
}
// Visa listans utseende efter sortering:
cout << "Listans utseende efter sortering:\n";
for(i1 = 0; i1 < 16; i1++) cout << iTal[i1] << " ";
cout << "\n\n";
}
Så här blir det när man kör programmet:
Övningsuppgift 7.7.1:
Nu ska vi ta och titta på den andra sorteringsalgoritmen. En algoritm är alltså den metodik ett program använder för att utföra en uppgift. I detta fall kallas den bubbelsortering. Här tittar man bara på två bredvid varandra liggande element i listan hela tiden, varvid det räcker med ett index. Låt oss kalla indexet 'i'. Då kan vi alltså jämföra element i med element i + 1. Det är två bredvid varandra liggande element. Om det vänstra innehåller ett tal som är större än det som ligger i det högra låter man talen byta plats. Man kan låta i 'bläddra igenom' listan i en for-slinga, men man måste avbryta den när i + 1 är siste elementet i listan. Annars blir det fel. Vi kan testa detta på listan i fråga:
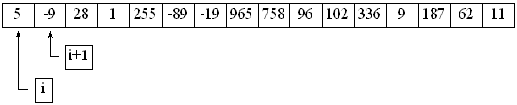
Här ser vi att 5 och -9 ska byta plats. Därefter ökar vi i med 1:
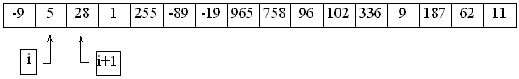
5:an i sin nya position ska alltså inte byta plats med 28, det är bara att gå vidare:

Däremot byter 1:an plats med 28. Fortsätter vi på samma sätt blir det så här när vi kommit till slutet av listan:
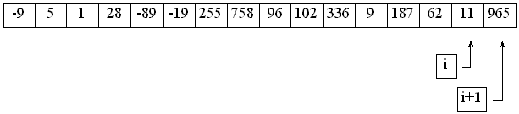
Listan är inte rätt sorterad, men talen ligger i en bättre ordning än förut. Nu är det bara att upprepa detta om och om igen tills listan är rätt sorterad.
Den sortering vi gjorde förut, urvalssorteringen, resulterade ju i att vi hade två programslingor, en med ett index i1 och en med ett index i2. Lägg märke till att den senare programslingan genomlöptes alla sina 'varv' för varje varv i den förra. Man kan betrakta det som att vi har en yttre och en inre slingan. Den yttre slingan kommer över den inre i JSP-schemat. Vi har en liknande situation här vid bubbelsorteringen. Vi behöver löpa igenom listan med en inre slinga, men vi behöver upprepa proceduren ett antal gånger, tills listan är färdigsorterad, och därför behöver vi även en yttre slinga, vilken inte har något index, utan i stället avbryts när listan är färdigsorterad.
Hur ska vi då veta att listan är färdigsorterad? Skulle den vara det kommer den inre slingan inte att byta några värden. Man skulle alltså kunna ha en variabel som räknar hur många gånger byten sker, och avbryta den yttre slingan när den variabeln blir noll efter att den inre slingan gåtts igenom alla sina gånger. Viktigt är då alltså att ge räknaren värdet noll varje gång före den inre slingan startas.
Övningsuppgift 7.7.2:
Övningsuppgift 7.7.3: