7.
Operatoröverlagring och typomvandlingsfunktioner
· Operatoröverlagring.
· Räkna med bråk.
· Operatoröverlagring som ‘friend’.
· Konstruktor med förvalt argument för impliciv typomvandling.
· Typomvandlingsoperatorer.
· Tvetydig typomvandling.
Operatoröverlagring.
Genom operatoröverlagring kan man anpassa C++ operatorer nästan hur långt som helst. När man väl behärskar reglerna för operatoröverlagring kvarstår en betydligt viktigare utmaning, att lära sig använda det på ett meningsfullt, snyggt och icke förvillande sätt. Det sistnämnda är svårast.
När man använder objekt kan man inte förvänta sig att de vanliga operatorerna ska ge det resultat syntaxen antyder. Vi måste i många fall överlagra operatorer just för att de ska få den mening vi förväntar oss när vi skriver programmet. Jämför exemplet med tilldelningsoperatorns effekt på ett objekt av typen CText ovan.
Man kan överlagra nästan vilken operator som helst, undantagen är få: elementoperatorn ‘.’, räckviddsoperatorn ‘::’, villkorsoperatorn ‘?:’ samt en version av pekare-till-elementoperatorn ‘.*’. Den andra versionen av pekare-till-elementoperatorn, ‘->*’ är dock tillåten att överlagra.
Det är dock inte samma sak som att alla operatorer alltid är så lämpliga att överlagra, kom ihåg:
· Överlagra inte en operator så att den får en betydelse som står i konflikt med tidigare betydelse.
· Överlagra inte en operator så att den får en tvetydig betydelse.
· Överlagra inte en operator så att den får en otydlig betydelse.
· Överlagra inte en operator för att förenkla skrivarbetet, meningen är att överlagringen ska förbättra och förtydliga användningen av operatorn.
Har du tänkt på att det finns två olika operatorer ‘-’? Den ena är en aritmetrisk operator avsedd att skapa uttryck som utför subtraktion. Denna kräver en variabel på var sida. (Tvåställig operator, eng. binary operator.)
Den andra tillhör också aritmetiken, men den är avsedd att vända tecken på ett numeriskt värde. Denna kräver att det finns endast en variabel, och den ska stå till höger om operatorn. (Enställig operator, eng. unary operator.)
Det finns fler enställiga operatorer, t.ex boolsk ICKE, ‘!’ och logisk ICKE ‘~’.
Tänk på att det finns operatorer som sätts samman med mer än ett tecken, t.ex. icke lika med ‘!=‘ är inte en kombination av boolsk ICKE och tilldelningsoperatorn, den är snarare att betrakta som ett reserverat ord för en operator. Även ‘[]’ och ‘()’ är operatorer och kan överlagras.
Kompilatorns regler för överlagring är betydligt enklare än de ovanstående. Följande förbud gäller:
· Man kan inte skapa nya operatorer genom att kombinera gamla. Det går t.ex. inte att skapa en operator ‘**’ för exponentiering.
· Man kan inte ändra en operators ‘ställighet’, d.v.s. en enställig operator måste förbli en enställig operator etc.
· Man kan inte ändra prioritetsordningen för en operator. Ska man överlagra en operator till att få en ny betydelse, måste man välja en som har en lämplig position i prioritetsordningen. Operatorn för bitvis exclusivt ELLER, ‘^’ har t.ex. alldeles för låg prioritet för att kunna användas som exponentieringsoperator. Trots att den ger en tydlig association till exponentiering kommer den att fungera fel i aritmetriska uttryck.
· Vissa operatorer av samma prioritet beräknas från vänster till höger, t.ex. ‘+’ och ‘-’ medan andra räknas från höger till vänster, t.ex. ‘=‘. Denna s.k. ‘associativa’ prioritet kan inte ändras.
· Man kan inte ändra en operators inverkan på de fördefinierade typerna, int, float, char etc.
·
Som redan nämnts kan man inte överlagra
följande operatorer:
‘.’ ‘.*’ ‘::’ ‘?:’
Räkna med bråk.
Hur mycket blir 1/3 + 1/3 + 1/3? Frågar man datorn blir det 0.99999! Gör man många sådana här beräkningar växer felet efterhand, och resultatet kan bli helt otillfredsställande. Låt oss därför skapa en klass som hanterar bråktal så som vi själva gör det.
Hur tänker vi när vi beräknar ovanstående? Vi tar tre stycken tredjedelar och slår ihop dem till 3/3, vilket även datorn får till 1. Hur gjorde datorn då? Den beräknade 1/3 till 0.33333. Därefter blev 0.33333 + 0.33333 + 0.33333 = 0.99999.
Lösningen ligger alltså i att hantera ett bråk som två tal, täljaren och nämnaren, och utföra beräkningarna i så logisk ordning som möjligt. Så länge vi har täljaren och nämnaren kvar är talet exakt. Skulle vi behöva operera på bråktal med olika nämnare måste vi omvandla enligt principen minsta gemensamma nämnare, så det lägger vi in i klassen som en privat metod. Så här kan vi t.ex. göra:
#include
<iostream.h>
#include
<stdlib.h>
#include
<math.h>
// Klasshuvud för klassen CBrak (Bråk)
class CBrak
{
public:
CBrak();
CBrak(long taljare, long namnare);
void Skriv() const;
CBrak operator+(const CBrak &h)
const;// h = höger operand!
private:
static long mgn(long v, long h); // Ger minsta gemensamma
// nämnare, v = vänster
long m_Taljare; // operand.
long m_Namnare;
};
// Förvald konstruktor.
CBrak::CBrak()
{
m_Taljare = 0;
m_Namnare = 1;
}
Nämnaren bör nog inte vara 0, så den initierar vi till 1 för att undvika eventuellt divisionsspill. Nästa konstruktor kräver lite arbete för att behålla dataintegriteten, och för att hantera negativa tal. Vi tar även mgn() till hjälp för att inte lagra tal med onödigt stor nämnare, t.ex. 3/12 lagas som 1/4:
// Konstruktor som tar täljare och nämnare som argument.
CBrak::CBrak(long taljare, long namnare)
{
int faktor; // Faktor att eventuellt förkorta bråket med.
if(namnare == 0) namnare = 1; // Skydd mot divisionsspill.
m_Taljare = taljare;
m_Namnare = namnare;
if(namnare < 0) // Flytta minustecknet till täljaren eller
{ // motverka två minustecken.
m_Taljare = -m_Taljare;
m_Namnare = -m_Namnare;
}
faktor = mgn(taljare, namnare); // Alltid positiv, se mgn()
if(faktor > 1) // Förkorta eventuellt bråket.
{
m_Taljare /= faktor;
m_Namnare /= faktor;
}
}
// Utskrift.
void CBrak::Skriv() const
{
cout << m_Taljare << ‘/’ << m_Namnare;
}
// Överlagrad +
operator.
CBrak
CBrak::operator+(const CBrak &h) const
{
long faktor;
long mult1, mult2;
faktor = mgn(m_Namnare, h.m_Namnare);
mult1 = m_Namnare/faktor;
mult2 = h.m_Namnare/faktor;
return CBrak(m_Taljare * mult2 +
h.m_Taljare * mult1,
m_Namnare * mult2);
}
// Minsta Gemensamma nämnare ger en faktor att dividera med.
// Funktionen använder en iterativ version av Euklides
// algoritm.
long
CBrak::mgn(long v, long h)
{
int temp;
v = labs(v); // Beräknar absolutvärdet.
h = labs(h);
while(h > 0)
{
temp = v % h;
v = h;
h = temp;
}
return v;
}
Funktionen mgn() beräknar egentligen inte minsta gemensamma nämnare, utan största faktor man kan använda för att förkorta bråket. Sedan får den funktion som anropar mgn() själv dividera täljare och nämnare med denna faktor. Så här skulle man kunna testa klassen:
void main()
{
CBrak a;
CBrak b(3, 4);
CBrak c(1, 3);
a = b + c;
b.Skriv();
cout << ” + ”;
c.Skriv();
cout << ” = ”;
a.Skriv();
cout << ”\n\n”;
}
Ovanstående exempel borde ge följande utskrift:
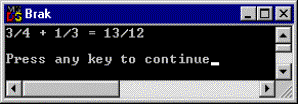
Uttrycket ‘b + c’ tolkas av kompilatorn som b.operator+(c), d.v.s. operator+ kallas för objekt b med objekt c som argument. Vill vi kunna lägga till ett heltal till ett objekt av typ CBrak behöver vi en operatoröverlagring som tar ett heltal som argument:
CBrak
CBrak::operator+(long h) const
{
return CBrak(m_Taljare + h * m_Namnare, m_Namnare);
}
Härigenom kan vi skriva så här:
a = b + 7;
Däremot kan vi inte ha ett heltal på höger
sida:
a = 7 + b; // Fel! 7 är inget objekt, ‘+’ tolkas som vanligt.
Detta skulle tolkas som:
a =
7.operator+(b);
Vilket kanske inte är så lyckat eftersom ‘7’ inte är något objekt och inte har någon operatoröverlagring!
Övningsuppgift:
· Skapa projetet Brak och klassen CBrak så som vi diskuterat ovan inklusive den överlagrade operatorn ‘operator+’.
· Skriv main() och testa att lägga ihop två bråktal som på sidan 6.
Övningsuppgift:
· Öppna projektet Brak om det inte redan är öppet.
· Ändra utskriftsmetoden så att nämnaren inte skrivs ut när den är 1. Tidigare skrev den t.ex. 3/1, vilket skulle se snyggare ut som 3.
· Lägg till överlagrade operatorer för subtraktion, multiplikation och division.
· Lägg till operationer i main() som testar de nya operatorerna.
Övningsuppgift:
· Öppna projektet Brak om det inte redan är öppet.
· Deklarera en konstruktor som tar ett långt heltal som argument.
· Lägg till följande operationer:
a = b + 7;
a = b - 7;
a = b * 7;
a = b / 7;
· Testa att det fungerar.
Övningsuppgift:
· Nederst på sidan 6 försöker vi addera ett CBrak-objekt till en konstant. Testa detta i main() och läs felmeddelandet. Vi ska rätta till problemet i nästa avsnitt.
Operatoröverlagring som ‘friend’.
En andra överlagring där vi använder oss av ‘friend’ kan lösa situationen åt oss. Vi kan deklarera en överlagring som tar såväl vänster som höger operand som argument. Om vänster operand deklareras som långt heltal har vi täckt upp ovanstående situation. Vi måste dock överlagra globalt, så att vi når operatorn tillsammans med 7:an ovan, eller vilket heltal som helst. Därför måste vi deklarera den som ‘friend’ i klassen, så att den globala funktionen får tillgång till klassens metoder:
// Tillägg i klasshuvudet.
friend CBrak
operator+(long v, const CBrak &h);
// Globalt deklarerad operatoröverlagring.
CBrak
operator+( long v, const CBrak &h)
{
return CBrak(h.m_Taljare + v * h.m_Namnare, h.m_Namnare);
}
Nu ska det gå bra att skriva:
a = 7 + b;
Vi har hela tiden tillgodosett kravet på att vi inte förändrar +tecknets tvåställighet, trots att vi fått olika antal argument i våra olika operatoröverlagringar. När operator+ definieras som medlemsfunktion i en klass blir klassens objekt det första ledet i tvåställigheten, men när vi deklarerar globalt måste båda ställen (d.v.s. till vänster respektive höger om +tecknet) anges som argument.
Samma resonemang gäller för enställiga operatorer. Då får man inte ange några argument alls i de deklarationer som står i klassen, medan den globala ska ha ett enda.
Övningsuppgift:
· Öppna projektet Brak om det inte redan är öppet.
· Deklarera den globala operatoröverlagringen för operator+ enligt ovan.
· Deklarera operatoröverlagringsfunktionen som friend till klassen.
· Kompilera, länka och testa. Nu ska det fungera, även ‘a = 7 + b’ som vi fick fel på tidigare.
Vi kan naturligtvis fortsätta med att definiera meningsfulla operatoröverlagringar för flera andra operatorer. De fyra räknesätten skulle i så fall generera tolv nya funktioner, fyra för klassens lokala operatorer, åtta för de globala operatorerna, med olika argumentlistor (CBrak, long / long, CBrak). Förutom dessa kan det bli fler, om man vill hantera =, +=, -=, *= och /=, vi kan åtminstone testa att överlagra operator= för Cbrak respektive long.
Vi testar att deklarera följande 14 operatoröverlagringar, varav en del redan är klara:
· Två globala överlagringar för varje räknesätt, en överlagring som tar en ‘long’ som vänster operand och ett ‘const CBrak &’ som höger operand, och en överlagring som tar ett ‘const CBrak &’ som vänster operand och en ‘long’ som höger operand. (Den första är redan gjord.)
· Två klasspecifika överlagringar av ‘operator=‘, en överlagring som tar ett ‘const CBrak &’ som operand och en överlagring som tar en ‘long’ som operand.
· En klasspecifik överlagring för varje räknesätt, vilken var och en tar ett’const CBrak&’ som argument.
Övningsuppgift:
· Öppna projektet Brak om det inte redan är öppet.
· Lägg till de operatoröverlagringar som nämnts i listan ovan.
· Lägg till beräkningar i main() enligt nedanstående utskrift:
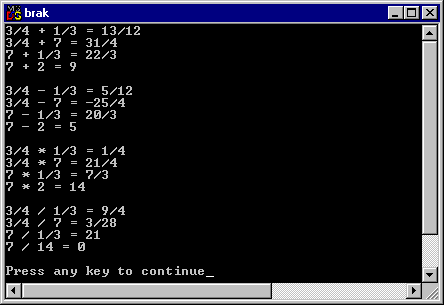
Obeservera att den sista beräkningen inte blir så bra. Vi får en implicit typomvandling när kompilatorn beräknar 7/14 i förväg, och som heltal blir detta noll.
Konstruktor med förvalt argument för implicit typomvandling.
Man kan nu undra om det är korrekt att överlagra samma operator mer än en gång. Faktum är att reglerna för polymorfism träder i kraft här. Det är tillåtet att ange samma operator flera gånger så länge argumentlistan skiljer sig. Vi har således inte helt och hållet uteslutit den vanliga +operatorn i och med den globala operatoröverlagringen, den nya operatorn gäller endast när man adderar ett objekt av typen CBrak till ett heltal. Samma sak gäller inom klassen.
Men vill vi minska på antalet överlagringar får vi inte glömma att vi har de förvalda argumenten att tillgå när vi överlagrar operatorer precis som i alla andra funktionsbeskrivningar. Reglerna för implicit typomvandling, d.v.s. de tillfällen kompilatorn automatiskt utför typomvandling, är dessa:
· Vid tilldelning, när man t.ex. tilldelar en variabel av typen long ett heltal.
· Vid aritmetriska operationer, om man t.ex. adderar ett heltal och ett flyttal konverteras först heltalet till flyttal.
· När ett argument passeras till en funktion, om man t.ex. skickar ett heltal till en funktion som tar ett långt heltal.
· När man returnerar ett värde från en funktion. Om funktionen t.ex. returnerar ett flyttal som tilldelas ett flyttal med dubbel precision.
Av detta kan vi utnyttja den tredje punkten, implicit typomvandling av argument som skickas till en konstruktor. Vi skulle t.ex. kunna skriva funktionsprototypen för vår konstruktoröverlagring så här:
// Ändring i klasshuvudet.
CBrak(long taljare, long namnare = 1);
// Cbrak &operator=(long h); Tag bort denna!
Nu behöver vi inte längre alla de operatoröverlagringar vi deklarerade tidigare. Vi behöver bara en operator för varje räknesätt, förutsatt att den tar två objekt av typen CBrak som argument, ett för höger och ett för vänster operand. Operator+ får t.ex. ett heltal som argument. Kompilatorn skapar lämpligt objekt, CBrak, och anropar konstruktorn med förvalt argument: nämnaren blir 1.
Får operator+ i stället två CBrak-objekt som
argument sker ingen typomvandling, medan två heltal inte tolkas som två
argument: kompilatorn beräknar i stället uttrycket före omvandling.
Implicit typomvandling från heltal till CBrak i kombination med det förvalda
argumentet i konstruktorn tar hand om alla nedanstående fall, tillsammans med
det förvalda argumentet:
CBrak a;
CBrak b(3,4);
CBrak c(1,3);
a = b + c; // OK, tolkas som det står.
a = b + 7; // OK, tolkas som a = b + CBrak(7);
a = 7 + b; // OK, tolkas som a = CBrak(7) + b;
a = 7 + 2; // OK, tolkas som a = CBrak(9);
I det sistnämnda fallet skapar kompilatorn en temporär variabel av typen long. Den i sin tur typomvandlas till CBrak.
Ovanstående metod drar nytta av konstruktorns förmåga att automatiskt typomvandla sina argument, i kombination med det förvalda argumentet. När kompilatorn läser uttrycken söker den upp en lämplig ‘operator+’, vilket vi ju redan har deklarerat globalt, och ändrar argumentlistan:
// Ändring i klasshuvudet.
friend CBrak
operator+(const CBrak &v, const CBrak &h);
// Ändring vid operatoröverlagringen.
// Globalt deklarerad operatoröverlagring.
CBrak
operator+(const CBrak &v, const CBrak &h)
{
long faktor;
long mult1, mult2;
faktor = v.mgn(v.m_Namnare, h.m_Namnare);
mult1 = v.m_Namnare/faktor;
mult2 = h.m_Namnare/faktor;
return CBrak(v.m_Taljare * mult2 +
h.m_Taljare * mult1,
v.m_Namnare * mult2);
}
Det är alltså fortfarande denna som sköter jobbet åt oss, men vi behöver bara en global överlagring för varje räknesätt och vi behöver inte längre den lokala operatoröverlagringen av ‘operator+’.
Övningsuppgift:
· Ta bort den konstruktor som tar ett argument.
· Ändra den konstruktor som tar två argument till att ha det andra argumentet förvalt till 1.
· Ta bort de lokala operatoröverlagringarna.
· Ta bort överlagringarna av operator=().
· Ta bort hälften av de globala operatoröverlagringarna så att du har fyra stycken kvar, en för varje räknesätt, och ändra de kvarvarande enligt ovanstående (koden ser annorlunda ut, så du får tänka till litet här).
· Testa alla fyra räknesätten p.s.s. som ovan.
· Så här kan utskriften se ut:
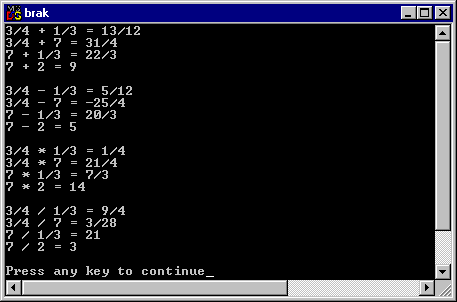
Observera att den sista raden inte ger ett
korrekt resultat. Detta beror av att den implicita typomvandlingen omvandlar
resultatet av 7/2, d.v.s. 3,5, till heltal. Kompilatorn skapar ju en temporär
variabel som innehåller 3,5 vilken direkt typomvandlas till heltal, varigenom
talet trunkeras till 3. Detta kan man lätt komma förbi om man typomvandlar
minst en av konstanterna till CBrak. Testa detta. Välj dessutom att ange en
division av heltal som kan förkortas, t.ex.
7 / 14. Vi kommer att få resultatet 1/2!
Typomvandlingsoperatorer.
Om man nu vill skicka ett objekt av typen CBrak som argument till en funktion som tar ‘float’ som argument, så behöver vi en operator till, en som sköter den omvandlingen. Även typomvandlingsoperatorn, ‘cast operator’ är en operator som kan överlagras. Låt oss testa med att överlagra typomvandling till ‘float’:
class CBrak
{
public:
...
operator float() const;
...
private:
...
};
// Deklaration av funktionskoden.
CBrak::operator
float() const
{
return (float)m_Taljare / (float)m_Namnare;
}
Föjande gäller för en typomvandlingsoperator:
· Observera att en typomvandling inte har någon returtyp, precis som konstruktor och destruktor deklareras de utan att man anger någonting alls.
· Den tar inga argument.
· Den måste deklareras som icke statisk medlemsfunktion.
· Den kan inte deklareras som ‘friend’.
Den överlagrade typomvandlingsoperatorn kallas om man använder någon av följande syntaxer:
float fTal;
int iTal;
CBrak cbTal(1,
3);
fTal = cbTal.operator float(); // Direkt anrop.
fTal = float(cbTal); // Syntax för konstruktoranrop.
fTal = (float)cbTal; // Syntax för typomvandling.
fTal = cbTal; // Automatiskt anrop.
iTal = cbTal; // Dubbel automatisk omvandling.
Observera att det sistnämnda fallet kräver två automatiska anrop, först ett till vår typomvandlare CBrak till float, sedan en för float till int. Kompilatorn klarar detta helt på egen hand.
Det går naturligtvis lika bra att konvertera från en klasstyp till en annan klasstyp. Har man en annan kompatibel klass, t.ex. en som hanterar flyttal med speciell notation, fast decimalpunkt för kronor och ören, teknisk notation e.d. så kan vi förse vår klass CBrak med en typomvandlare som gör att den kan acceptera sådana objekt som argument:
class CBrak
{
public:
...
operator CTekNot() const;
operator CKronOren() const;
...
};
Dessa operatorer skulle förse oss med automatisk typomvandling från CBrak till CTekNot respektive CKronOren.
Man kan även förse sin klass med typomvandlingsoperator avseende en klass man inte har källkoden till. Man får dock aldrig glömma att man själv har ansvar för att typomvandlingen i sig har någon mening. Därför krävs att man har viss insikt i den andra klassens arbetssätt.
När vi i början av detta avsnitt omvandlade ett bråktal till ett heltal förlorade vi information. Vid flyttalsomvandlingen blev det antagligen en eller flera decimaler, vilka helt enkelt trunkeras vid omvandling till heltal. Siffrorna i exemplet var 1/3, d.v.s. fTal blev 0,33333 medan iTal blev 0. Det är upp till oss att avgöra om detta är önskvärt eller ej.
Det skulle dock verka märkligt att omvandla ett CBrak-objekt till ett CText-objekt. Om man däremot själv har tillgång till CText kanske man kan skriva en konstruktor som tar ett CBrak-objekt och omvandlar till text. 1/3 skulle då kunna bli ”1/3” eller ”0,33333”, allt efter behov.
Övningsuppgift:
· Öppna projektet Brak om det inte redan är öppet.
· Behåll all kod i main()!
· Skapa en överlagrad typomvandling som gör att vi kan överlämna bråktalet som ett flyttal.
· Tilldela en flyttalsvariabel fTal i main() värdet av det beräknade bråket, och skriv ut direkt efter.
· Observera att alla beräkningar som innehåller en kombination av ett CBrak-objekt och en konstant inte längre går att kompilera. Det bör bli 8 st. Kommentera bort dem och tillhörande utskrifter, så ska vi diskutera det problemet i nästa avsnitt.
· Så här ska utskriften bli nu:
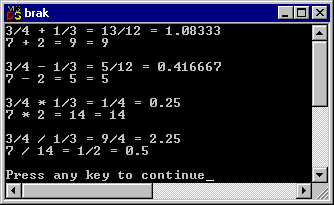
Tvetydig typomvandling.
När vi lade till en typomvandlingsoperator i klassen CBrak skapade vi faktiskt ett nytt problem. Titta på nedanstående tilldelning:
a = b + 7;
Den fungerade ju bra förut! Den tolkades som:
a = b +
CBrak(7);
Den kan fortfarande tolkas på detta sätt, men den nya typomvandlingsoperatorn ger oss faktiskt en tolkning till:
a = (float)b +
7;
Vilket ju också är korrekt. Kompilatorn har alltså två möjligheter att tolka detta (vilka bägge egentligen leder till samma resultat), den kan konvertera 7:an till CBrak-objekt och sedan använda CBrak:s överlagrade operator+ till att addera objekten enligt de regler vi fastställt, men den kan också börja med att konvertera b till flyttal, lägga till 7 och sedan tilldela a resultatet.
Error, ambiguous...
Båda metoderna ger ett någorlunda korrekt resultat, men kompilatorn genererar ett fel bara för att den inte vet hur den ska välja. Detta är i grund och botten bra, eftersom vi vill ha litet att säga till om i detta fall. När b omvandlas till float förlorar vi nämligen precision, och det var ju just det som klassen CBrak skulle hjälpa oss att undvika.
Det finns ett par sätt att lösa denna tvetydighet. Ett är att använda en vanlig medlemsfunktion för att utföra addition, i stället för den överlagrade operator+:
class CBrak
{
public:
...
friend CBrak add(const CBrak &v, const
CBrak &h);
...
};
Eftersom denna funktion heter add() och inte ‘+’ så uppstår inte tvetydigheten. Vi har i stället förlorat möjligheten att använda operatorn ‘+’.
En annan lösning vore att ta bort en implicit typomvandling. Vi skulle kunna ta bort den automatiska konverteringen från heltal till CBrak genom att ta bort den konstruktor som bara tar ett argument. Då skulle ovanstående sats behöva ändras till:
a = b +
CBrak(7,1);
...vilket kanske inte heller är så tillfredsställande. Skulle man sedan vilja addera värden som standardtyper måste man skriva så här:
a = CBrak(b +
7,1);
Inte heller lika snyggt. Man skulle kanske i stället ta bort den automatiska typomvandlingen från CBrak till flyttal genom att ändra typomvandlingsoperatorn till att vara en vanlig metod:
class CBrak
{
public:
...
float typFloat() const;
...
};
Nu kvarstår bara den ursprungliga tolkningen av vår addition:
a = b + 7; // Tolkas som a = b + CBrak(7);
Den andra tolkningen måste nu anges som ovanstående funktionsanrop i stället:
int iTal;
iTal = b.typFloat() + 7;
Sens moral: Var försiktig om du överlagrar operatorer i kombination med användning av implicit typomvandling.
Tvetydighet kan även uppstå när man deklarerar samma typkonvertering i mer än en klass:
class
CKronOren;
class CBrak
{
public:
...
CBrak(CKronOren belopp); // CKronOren -> CBrak!
...
};
class CKronOren
{
public:
...operator CBrak(); // CKronOren -> CBrak igen!
...
};
void main()
{
CBrak a;
CKronOren b(3, 50);
a = b; // Error, ambiguous...
// a = CBrak(b); eller a =
b.operator CBrak();?
}
Kompilatorn kan inte avgöra om den ska använda konstuktorn eller operatoröverlagringen. Man kan explicivt ange att den ska använda operatoröverlagringen, men inte att den ska använda konstruktorn:
a = b.operator CBrak(); // Använd den överlagrade operatorn.
a = CBrak(b); // Fel, fortvarande tvetydigt.
a = (CBrak)b; // Fel, fortfarande tvetydigt.
Denna sortens tvetydighet är lätt att undvika eftrsom den beror av att den som skrev den ene klassen känner till den andre och vice versa, det är antagligen samma person som skrivit bägge klasserna. Ta bort den ena konverteringsfunktionen så är problemet ur världen.
Tvetydighet kan även uppstå när två klasser deklarerar var sin konstruktor med liknande implicita typomvandlingar. Vi har t.ex. vårt projekt med CBrak:
// I klassen CBrak.
CBrak(float fTal);
Låt oss deklarera en global funktion som tar ett objekt av typen CBrak som argument:
void berakna(CBrak braktal);
Skapar vi sedan ett annat projekt för våra kronor och ören kanske vi deklarerar klassen CKronOren:
// I klassen CKronOren.
CKronOren(float fTal);
Även i den skapar vi en global funktion berakna():
void berakna(CKronOren belopp);
Skulle vi nu använda bägge dessa klasserna, där de respektive globala funktionerna berakna() följer med, så uppfattar kompilatorn det som att vi överlagrar funktionen berakna(). Argumentlistan skiljer sig ju.
Problemet uppstår när vi försöker anropa funktionen och samtidigt aktiverar typomvandling. Detta kan ske om bägge klasserna har konstruktorer som tar flyttal som argument, och konverterar till respektive klass:
berakna(3,5);
Ska detta tolkas som att berakna() ska ta 3 kronor och 50 öre som argument eller 3/5? Kompilatorn kan inte avgöra detta åt dig.
Problemet är inte helt lätt att förebygga. Två programmerare som kanske inte vet om varandra kan ha skrivit klasserna. Den ena klassen kanske kommer med vid köp av kompilatorn, t.ex. ingår i MFC, medan någon annan levererat den andra. Och där sitter du mitt emellan och fattar ½ 7 när kompilatorn säger:
Error, ambiguous...
Situationen blir ännu mer komplex när man tänker på att en programmerare skriver en klass som använder ett objekt av en annan klass där omvandlingen ingår som argument, eller bakar in klasserna i varandra etc. I slutändan kanske du använder en klass någon annan skrivit som på olika irrvägar innehåller en klass du själv skrivit, utan att du ens vet om att så är fallet.
För att minska sannolikheten för att tvetydighet ska uppstå bör man definiera implicita typkonverteringar bara där det är uppenbart att man borde göra det. Man kan alltid konvertera explicit genom att använda konstruktorer som tar mer än ett argument, eller genom att använda vanliga medlemsmetoder för typomvandling, som t.ex. typFloat() enligt ovan.
? C++ Language Reference - Overloaded Operators.